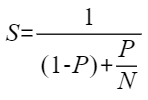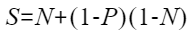理论计算极限

优化之前需明确，该次优化可获得多大收益。此处介绍两个定律，以在优化过程中进行简单理论评估。

• 阿姆达尔定律——强扩展性

  

  强扩展是指在规模固定的情况下，通过提高多处理器的数量来减少代码执行的时间。

  阿姆达尔定律（Amdahl's Law）解释了提升一个系统的一个部分的性能对整个系统有多大影响。公式中的参数含义如下。

  • S：加速比
  • P：可以并行化代码分数
  • N：并行部分可以得到的多处理器的数量

  通过公式可以得出：P越大，S即优化空间越大。在P很小的情况下，不论增加多少计算资源，整个优化收益都较小。

• 古斯塔夫森定律——弱扩展性

  

  弱扩展是指问题的规模可能会随着资源的增加而增加。

  可以用古斯塔夫森定律（Gustafson's law）来理论分析，公式参数同阿姆达尔定律。

  通过公式可以得出：随着N的增加，整个问题规模也越来越大。在优化时首先要分析问题归属场景，再根据每类场景对应公式做简单推测。

在优化过程当中，每一项指标都受到硬件的限制，以下介绍每个指标的理论峰值天花板。

• A100卡单精度FLOPS极限=（2倍FP64,1/4 FP16）：

  1410MHz内核时钟 * 1 GPU * (108多处理器 * 64 浮点计算/多处理器) * 2 ops/cycle = 19.5TFLOPS

• A100内存带宽极限：

  1GPU * 5120bit * 1215MHz内存时钟 * 2DDR / 8bits = 1555GB/s

一般来说，程序的内存带宽利用率达到40%~60%是一般水平，达到60%~75%则利用率较高，到75%以上则非常高，绝大部分GPU代码都受限于内存利用率。这里要提一下利特尔法则（Little's Law）：

L = λW

其中：

• L为系统中平均物体的数量
• W为物体在系统中的平均等待时间（逗留时间）
• λ为物体进入系统的速率

物体进入系统的速率是λ个每秒，整个系统一共保留了W秒的物体，因此整个系统里有L个物体。

系统中平均物体的数量，即一个物体在系统中逗留的那段时间里总共又进来了多少物体，等于物体进入系统的速率 * 物体的平均逗留时间。

对应到GPU代码优化上，传送的有用字节数 = 单位时间传送的字节数 * 带宽，那么要么降低每个内存事务的平均延迟时间，要么增大带宽。

不同的存储类型的访问时间如表1所示。

上述性能采用A100显卡数据，其他显卡性能请参考：https://sysrqmts.com/zh/gpus/compare/nvidia-a10-pcie-vs-nvidia-a100-sxm4-40-gb