?sy(he)evd
计算对称（Hermite）矩阵的全部特征值和特征向量（可选）。其中特征向量通过分治算法计算。
即矩阵A分解为：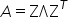
，其中
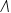为对角矩阵，对角线元素
为特征值；Z为正交矩阵，其每列向量
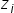为对应的特征向量。即
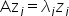，其中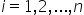
。
接口定义
C Interface：
void dsyevd_(const char *jobz, const char *uplo, const int *n, double *a, const int *lda, double *w, double *work, const int *lwork, int *iwork, const int *liwork, int *info);
void ssyevd_(const char *jobz, const char *uplo, const int *n, float *a, const int *lda, float *w, float *work, const int *lwork, int *iwork, const int *liwork, int *info);
void cheevd_(const char *jobz, const char *uplo, const int *n, float _Complex *a, const int *lda, float *w, float _Complex *work, const int *lwork, float *rwork, const int *lrwork, int *iwork, const int *liwork, int *info);
void zheevd_(const char *jobz, const char *uplo, const int *n, double _Complex *a, const int *lda, double *w, double _Complex *work, const int *lwork, double *rwork, const int *lrwork, int *iwork, const int *liwork, int *info);
Fortran Interface：
DSYEVD(JOBZ, UPLO, N, A, LDA, W, WORK, LWORK, IWORK, LIWORK, INFO);
SSYEVD(JOBZ, UPLO, N, A, LDA, W, WORK, LWORK, IWORK, LIWORK, INFO);
CHEEVD(JOBZ, UPLO, N, A, LDA, W, WORK, LWORK, RWORK, LRWORK, IWORK, LIWORK, INFO);
ZHEEVD(JOBZ, UPLO, N, A, LDA, W, WORK, LWORK, RWORK, LRWORK, IWORK, LIWORK, INFO);
参数
参数名 |
类型 |
描述 |
输入/输出 |
|---|---|---|---|
jobz |
字符型 |
|
输入 |
uplo |
字符型 |
|
输入 |
n |
整数型 |
对称矩阵A的行数或列数。 |
输入 |
a |
|
|
输入/输出 |
lda |
整数型 |
A的leading dimension大小，要求lda ≥max(1, n)。 |
输入 |
w |
|
按升序排列的特征值，长度为n。 |
输出 |
work |
|
临时存储空间，调用后work[0]为最优的lwork值。 |
输出 |
lwork |
整数型 |
work数组的长度。 lwork=-1时查询最优work大小，结果保存在work[0]中，否则：
|
输入 |
rwork（复数类型特有） |
|
临时存储空间，调用后work[0]为最优的lwork值。 |
输出 |
lrwork（复数类型特有） |
|
rwork数组的长度。 lwork=-1时查询最优work大小，结果保存在work[0]中，否则：
|
输入 |
iwork |
整数型数组 |
临时存储空间，使用lwork=-1调用后iwork[0]为最优的liwork值。 |
输出 |
liwork |
整数型 |
iwork数组的长度。 liwork=-1时查询最优iwork大小，结果保存在iwork[0]中，否则：
|
输入 |
info |
整数型 |
执行结果：
|
输出 |
依赖
#include "klapack.h"
示例
C Interface：
char jobz = 'V';
char uplo = 'L';
int n = 5;
int lda = 5;
int info = 0;
double w[5];
double *work = NULL;
double qwork;
int lwork = -1;
int *iwork = NULL;
int qiwork;
int liwork = -1;
/*
* Symmetric A (stored in column-major):
* 7.027 8.710 1.015 6.929 7.584
* 8.710 0.839 2.469 3.850 0.559
* 1.015 2.469 1.930 6.761 7.207
* 6.929 3.850 6.761 4.344 4.804
* 7.584 0.559 7.207 4.804 6.177
*/
double a[] = {7.027, 8.710, 1.015, 6.929, 7.584,
8.710, 0.839, 2.469, 3.850, 0.559,
1.015, 2.469, 1.930, 6.761, 7.207,
6.929, 3.850, 6.761, 4.344, 4.804,
7.584, 0.559, 7.207, 4.804, 6.177};
/* Query optimal work size */
dsyevd_(&jobz, &uplo, &n, a, &lda, w, &qwork, &lwork, &qiwork, &liwork, &info);
if (info != 0) {
return ERROR;
}
lwork = (int)qwork;
work = (double *)malloc(sizeof(double) * lwork);
liwork = (int)qiwork;
iwork = (int *)malloc(sizeof(int) * liwork);
/* Calculate eigenvalues and eigenvectors */
dsyevd_(&jobz, &uplo, &n, a, &lda, w, work, &lwork, iwork, &liwork, &info);
free(work);
free(iwork);
/*
* Output:
* Eigenvalues (in w)
* -8.8422 -3.3411 1.1888 6.2050 25.1065
* Eigenvectors (in a, stored in column-major)
* 0.5405 -0.1616 -0.3059 -0.5235 -0.5604
* -0.4913 0.5975 0.2432 -0.4882 -0.3228
* 0.4886 0.4989 0.3454 0.5213 -0.3482
* -0.2410 -0.6062 0.5831 0.1038 -0.4729
* -0.4120 0.0219 -0.6228 0.4528 -0.4867
*/
Fortran Interface：
CHARACTER :: jobz = "V"
CHARACTER :: uplo = "L"
PARAMETER (n = 5)
PARAMETER (lda = 5)
INTEGER :: info = 0
REAL(8) :: w(5);
REAL(8) :: qwork(1)
REAL(8), ALLOCATABLE :: work(:)
INTEGER :: lwork = -1
INTEGER :: qiwork(1)
REAL(8), ALLOCATABLE :: iwork(:)
INTEGER :: liwork = -1
* Symmetric A (stored in column-major):
* 7.027 8.710 1.015 6.929 7.584
* 8.710 0.839 2.469 3.850 0.559
* 1.015 2.469 1.930 6.761 7.207
* 6.929 3.850 6.761 4.344 4.804
* 7.584 0.559 7.207 4.804 6.177
REAL(8) :: a(n, n)
DATA a / 7.027, 8.710, 1.015, 6.929, 7.584,
$ 8.710, 0.839, 2.469, 3.850, 0.559,
$ 1.015, 2.469, 1.930, 6.761, 7.207,
$ 6.929, 3.850, 6.761, 4.344, 4.804,
$ 7.584, 0.559, 7.207, 4.804, 6.177 /
* Query optimal work size
EXTERNAL DSYEVD
CALL DSYEVD(jobz, uplo, n, a, lda, w, qwork, lwork, qiwork,
$ liwork, info)
IF (info.NE.0) THEN
CALL EXIT(1)
END IF
lwork = INT(qwork(1))
liwork = INT(qiwork(1))
ALLOCATE(work(lwork), iwork(liwork))
* Calculate eigenvalues and eigenvectors
CALL DSYEVD(jobz, uplo, n, a, lda, w, work, lwork, iwork,
$ liwork, info)
DEALLOCATE(work, iwork);
* Output:
* Eigenvalues (in w)
* -8.8422 -3.3411 1.1888 6.2050 25.1065
* Eigenvectors (in a, stored in column-major)
* 0.5405 -0.1616 -0.3059 -0.5235 -0.5604
* -0.4913 0.5975 0.2432 -0.4882 -0.3228
* 0.4886 0.4989 0.3454 0.5213 -0.3482
* -0.2410 -0.6062 0.5831 0.1038 -0.4729
* -0.4120 0.0219 -0.6228 0.4528 -0.4867
