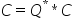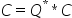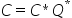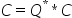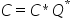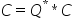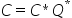优化的LAPACK函数
对优化的LAPACK的所有函数族进行描述。
功能 |
函数族 |
数据类型 |
描述 |
|---|---|---|---|
矩阵分解 |
?getrf |
s,d,c,z |
计算矩阵的LU分解,允许行交换。 |
?geqrf |
s,d,c,z |
矩阵QR分解。 |
|
?gerqf |
s,d,c,z |
矩阵RQ分解。 |
|
?geqlf |
s,d,c,z |
矩阵QL分解。 |
|
?gelqf |
s,d,c,z |
矩阵LQ分解。 |
|
?potrf |
s,d,c,z |
实对称或共轭对称正定矩阵的Cholesky分解。 |
|
?pttrf |
s,d,c,z |
计算实(共轭)对称正定三对角矩阵A的LDL*或U*DU分解。 |
|
?gttrf |
s,d,c,z |
计算一般三对角矩阵A的LU分解。 |
|
?sptrf |
s,d,c,z |
计算压缩对称矩阵的LDL*或U*DU分解。 |
|
?hptrf |
c,z |
计算压缩Hermite矩阵的LDL*或U*DU分解 |
|
?pptrf |
s,d,c,z |
计算压缩存储的对称正定矩阵的LLT或UTU分解。 |
|
线性方程组求解 |
?ppsv |
s,d,c,z |
压缩存储实对称或共轭对称正定矩阵的Cholesky分解。 |
?gesv |
s,d,c,z |
通过LU分解的结果来求解线性方程组。 |
|
?ptsv |
s,d,c,z |
求解线性方程组,其中系数矩阵A为实(共轭)对称正定三对角矩阵。 |
|
?gtsv |
s,d,c,z |
求解线性方程组A*X=B,其中系数矩阵A为一般三对角矩阵。 |
|
?posv |
s,d,c,z |
求解线性方程组A*X=B,其中系数矩阵A为实对称或共轭对称正定矩阵。 |
|
矩阵求逆 |
?getri |
s,d,c,z |
根据?getrf结果计算逆矩阵。 |
?potri |
s,d,c,z |
根据?potrf结果计算逆矩阵。 |
|
?pptri |
s,d,c,z |
根据?pptrf结果计算逆矩阵。 |
|
?trtri |
s,d,c,z |
计算上/下三角矩阵的逆矩阵。 |
|
回代求解 |
?pttrs |
s,d,c,z |
求解三对角方程AX=B,其中系数矩阵A由?pttrf分解而来。 |
?ptts2 |
s,d,c,z |
求解三对角方程AX=B,其中系数矩阵A由?pttrf分解而来。 |
|
?gttrs |
s,d,c,z |
求解三对角方程A*X=B,或A**T *X=B,或A**H *X=B,其中系数矩阵A由?gttrf分解而来。 |
|
?gtts2 |
s,d,c,z |
求解三对角方程A*X=B,或A**T *X=B,或A**H *X=B,其中系数矩阵A由?gttrf分解而来。 |
|
?trtrs |
s,d,c,z |
求解三角方程A * X = B或A**T * X = B。 |
|
?getrs |
s,d,c,z |
求解一般线性方程AX=B,其中系数矩阵A由?getrf分解而来。 |
|
?pptrs |
s,d,c,z |
求解压缩存储的对称正定线性方程AX=B,其中系数矩阵A由?pptrf分解而来。 |
|
特征值问题 |
?(sy/he)evd |
s,d,c,z |
计算实对称(Hermite)矩阵特征值和特征向量,其中特征向量通过分治算法计算。 |
?(sy/he)ev |
s,d,c,z |
计算实对称(Hermite)矩阵特征值和特征向量。 |
|
?steqr |
s,d,c,z |
使用QL或QR方法求解对称三对角矩阵的特征值和特征向量。 |
|
?stedc |
s,d,c,z |
对称(Hermite)三对角矩阵的特征值求解,Divide-and-Conquer 算法 |
|
奇异值问题 |
?gesvd |
s,d,c,z |
一般矩阵SVD分解 |
?gebrd |
s,d,c,z |
一般矩阵变换到两对角矩阵 |
|
?bdsdc |
s,d |
两对角矩阵的 SVD 分解, Divide-and-Conquer |
|
?gesdd |
s,d,c,z |
一般矩阵SVD分解, Divide-and-Conquer |
|
?bdsqr |
s,d |
两对角矩阵的 SVD 分解 |
|
最小二乘问题 |
?gels |
s,d,c,z |
使用矩阵的QR或LQ分解来求解超定或欠定线性方程组。 |
?gelss |
s,d,c,z |
使用SVD方法对线性最小二乘问题求解其最小范数解。 |
|
?gelsd |
s,d,c,z |
使用分治法对线性最小二乘问题求解其最小范数解。 |
|
其他 |
?(or,un)glq |
s,d,c,z |
生成具有正交行的实/复矩阵Q,其中计算Q的H由?gelqf返回的。 |
?(or,un)gqr |
s,d,c,z |
生成具有正交行的实/复矩阵Q,其中计算Q的H由?geqrf返回的。 |
|
?(or,un)grq |
s,d,c,z |
生成具有正交行的实/复矩阵Q,其中计算Q的H由?gerqf返回的。 |
|
?(or,un)gql |
s,d,c,z |
生成具有正交列的实/复矩阵Q,其中计算Q的H由?geqlf返回的。 |
|
?(or,un)mlq |
s,d,c,z |
计算 |
|
?(or,un)mqr |
s,d,c,z |
计算 |
|
?(or,un)mql |
s,d,c,z |
计算 |
|
?(or,un)mrq |
s,d,c,z |
计算 |
|
?sy(he)trd |
s,d,c,z |
将对称矩阵或Hermite矩阵通过相似变换成对称三对角T。 |
|
?sy(he)trd_2stage |
s,d,c,z |
将对称矩阵A转为对称三对角矩阵T,即A**T*A*Q=T,其中Q为正交矩阵。 |
|
?lasr |
s,d,c,z |
对矩阵A做平面旋转操作。 |
|
?(or,un)mbr |
s,d,c,z |
计算C=Q*C或Q**T*C或C*Q或C*Q**T或C=P*C或P**T*C或C*P或C*P**T,其中正交矩阵Q和P**T由函数GEBRD计算得到,即A=Q*B*P**T。 |
|
?(or,un)gtr |
s,d,c,z |
通过反射因子生成正交矩阵Q,其中反射因子由SYTRD计算得来。 |
|
辅助函数 |
?laset |
s,d,c,z |
初始化m*n的矩阵,且将对角线元素设置为beta,非对角线元素设置为alpha。 |
?laswp |
s,d,c,z |
对矩阵做一系列的行交换操作。 |
|
?lascl |
s,d,c,z |
对矩阵做scalar操作。 |
|
?lange |
s,d,c,z |
计算矩阵的范数(包含:1范数,F范数,无穷范数等)。 |
|
?lacpy |
s,d,c,z |
拷贝矩阵A的所有元素或部分元素到矩阵B。 |
|
混合精度线性方程组求解 |
?gesv |
zc,ds |
用混合精度法来求解一般线性方程组。 |