WinKaiser

给指定向量加Kaiser窗。其具体公式为：

$\text{[math]}$

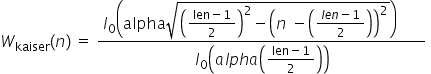
I₀()表示第一类修正的0阶贝塞尔函数，计算公式如下：

$\text{[math]}$

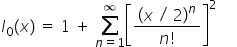
函数接口声明如下：

整型数的操作：
HmppResult HMPPS_WinKaiser_16s(const int16_t* src, int16_t* dst, int32_t len, float alpha);

HmppResult HMPPS_WinKaiser_16sc(const Hmpp16sc* src, Hmpp16sc* dst, int32_t len, float alpha);

浮点数的操作：
HmppResult HMPPS_WinKaiser_32f(const float* src, float* dst, int32_t len, float alpha);

HmppResult HMPPS_WinKaiser_64f(const double* src, double* dst, int32_t len, double alpha);

HmppResult HMPPS_WinKaiser_32fc(const Hmpp32fc* src, Hmpp32fc* dst, int32_t len, float alpha);

HmppResult HMPPS_WinKaiser_64fc(const Hmpp64fc* src, Hmpp64fc* dst, int32_t len, double alpha);

整型数的原址操作：
HmppResult HMPPS_WinKaiser_16s_I(int16_t* srcDst, int32_t len, float alpha);

HmppResult HMPPS_WinKaiser_16sc_I(Hmpp16sc* srcDst, int32_t len, float alpha);

浮点数的原址操作：
HmppResult HMPPS_WinKaiser_32f_I(float* srcDst, int32_t len, float alpha);

HmppResult HMPPS_WinKaiser_64f_I(double* srcDst, int32_t len, double alpha);

HmppResult HMPPS_WinKaiser_32fc_I(Hmpp32fc* srcDst, int32_t len, float alpha);

HmppResult HMPPS_WinKaiser_64fc_I(Hmpp64fc* srcDst, int32_t len, double alpha);

参数

参数名	描述	取值范围	输入/输出
src	指向源向量的指针。	非空	输入
dst	指向目的向量的指针。	非空	输出
srcDst	指向原址操作向量的指针。	非空	输入/输出
len	向量长度。	(0,INT_MAX]	输入
alpha	与Kaiser窗方程相关的可调参数。	alpha是double类型时，需要满足fabs(alpha)(len-1)/2<=308。 alpha是float类型时，需要满足fabs(alpha)(len-1)/2<=38。	输入

返回值

成功：返回HMPP_STS_NO_ERR。
失败：返回错误码。

错误码

错误码	描述
HMPP_STS_NULL_PTR_ERR	src、dst、srcDst这几个入参中存在空指针。
HMPP_STS_SIZE_ERR	len小于1。
HMPP_STS_HUGEWIN_ERR	Kaiser window的值太大。 alpha是double类型时，fabs(alpha)(len-1)/2>308。 alpha是float类型时，fabs(alpha)(len-1)/2>38错误。

描述

HMPP_STS_NULL_PTR_ERR

src、dst、srcDst这几个入参中存在空指针。

HMPP_STS_SIZE_ERR

len小于1。

HMPP_STS_HUGEWIN_ERR

Kaiser window的值太大。

alpha是double类型时，fabs(alpha)*(len-1)/2>308。
alpha是float类型时，fabs(alpha)*(len-1)/2>38错误。

示例

#define BUFFER_SIZE_T 10

int main()
{
    int16_t src[BUFFER_SIZE_T] = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19};
    float alpha = 0.5;  
    int16_t dst[BUFFER_SIZE_T];
    (void)HMPPS_Zero_16s(dst, BUFFER_SIZE_T); // 数组初始化，将dst所有元素初始化为0.

    HmppResult result = HMPPS_WinKaiser_16s(src, dst, BUFFER_SIZE_T, alpha);
    printf("result = %d\n", result);
    if (result != HMPP_STS_NO_ERR) {
        return -1;    
    }

    printf("dst =");
    for (int32_t i = 0; i < BUFFER_SIZE_T; i++) {
        printf(" %d", dst[i]);   
    }
    printf("\n");

    return 0;
}

运行结果：

result = 0
dst = 4 6 9 12 14 15 15 13 10 7

父主题： 基础与通用运算