社团挖掘

场景介绍

社团挖掘，就是要在一个图（包含顶点和边）上发现群体结构，也就是要把图中的结点进行聚类，构成一个个的群体（社团/社区）。一般认为社团内部的点之间的连接相对稠密，而不同社团的点之间的连接相对稀疏。

算法原理

• MCE算法

  MCE（Maximal Clique Enumeration，极大团）算法是在大规模图数据中，精确求解所有的极大团，其中极大团的定义如下：团是图中一个两两之间有边的顶点集合。如果一个团不被其他任何一个团包含，那么这个团即为极大团。

• WCE算法

  WCE （Weak Clique Enumeration，弱团）是一种重叠社团挖掘的算法，在社交网络中是一个很重要的研究。所谓的弱团挖掘，即利用检测到的三角形结果，如果两个三角形有一条边是重叠的，则将两个三角形合并在一起，并递归的合并下去，最终到不能合并为止。

• SCC算法

  SCC（Strongly Connected Components，强联通分量）算法是图计算领域的基础算法。在有向图中，强连通图是指每一个顶点皆可以经由该图上的边抵达其他的每一个点的有向图，即对于图上的每一个点对(V_a, V_b )，都有V_a→V_b以及V_b→V_a。强连通分量则是指有向图的极大强连通子图。

• Louvain算法

  Louvain算法作为一种以最大化模块度（Modularity）数值为目标函数的一种社区检测方法，具有社区检测效果好、速度快等特点。其主要通过贪心算法的策略，从底层不断聚合结点，每一次结点的聚合都选择能够使当前模块度增益最大的操作，从而最终达到社区划分结果在模块度评价指标上的最优解。

• LPA算法

  LPA（Label Propagation，标签传播）算法是图分析领域的经典算法，主要利用邻居的标签信息在网络图中传播而进行非重叠社团划分。

• CC算法

  CC（Connected Components，连通分量）算法是图计算领域的基础算法，用于求解无向图的所有连通分量。其中连通分量的定义如下：连通分量是指无向图中的极大连通子图，即子图中的任意点都可以通过边互相抵达，且与子图外的任意点不能互相抵达。本算法基于Spark计算引擎，精确求解所有连通分量。

编程实例

本示例以MCE（极大团）算法来介绍编程示例。

run API

• API

  1	run[T: ClassTag](graph: RDD[(T, T)], minK: Int, maxDegree: Int, repartition: Int): (RDD[(Int, T)], RDD[(Int, String)])

• 功能描述

  根据指定过滤条件计算关系网络中极大团信息。

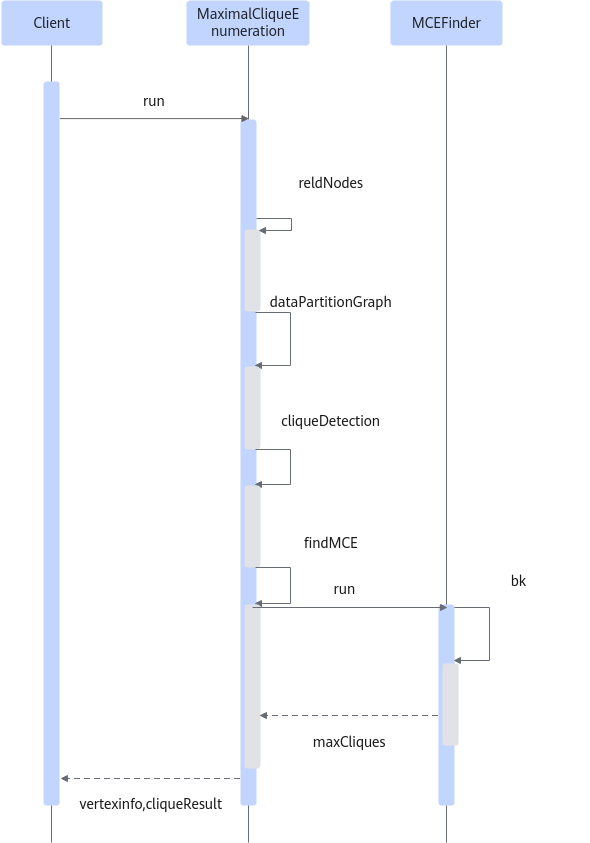
  MCE算法时序图如图1所示。

  图1 MCE算法时序图
  

• API描述
  1. 包名：package org.apache.spark.graphx.lib
  2. 类名：MaximalCliqueEnumeration
  3. 方法名：run
  4. 参数：如表1所示。

     表1 参数详情

     参数名称	取值类型	描述
     graph	RDD[(T, T)]	图边数据
     minK	Int如3等	最小的极大团结点规模
     maxDegree	Int如2000等	结点最大度数（指和该结点相关联的边的条数）
     repartition	Int如100等	计算时的分区个数
     T	String、Int、Long	结点类型

  5. 输出：

     RDD[(Int , T)]——结点映射关系：新结点ID 原结点ID

     RDD[(Int, String)]——结点所属极大团：新结点ID 极大团编号

• 使用MCE样例

  1 2 3 4 5 6 7 8 9

  val conf = new SparkConf().setAppName("Maximal Clique Detection") val sc = new SparkContext(conf) val inputData = Array( ("1", "2"), ("1", "3"), ("2", "3"), ("1", "4")) val inputDataRdd = sc.parallelize(inputData) MaximalCliqueEnumeration.run(inputDataRdd, 3, 2000, 1)

• 样例结果
  • 结点映射结果

    0,4
    1,2
    2,3
    3,1

  • 极大团结果

    1,c1
    2,c1
    3,c1